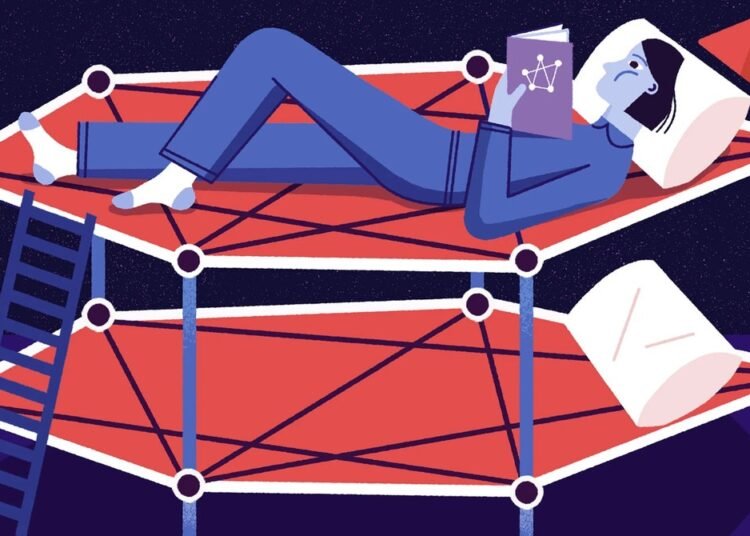
The bunkbed conjecture, a well-known hypothesis in probability theory, has recently been disproven by a team of mathematicians. This conjecture, which deals with navigating stacked graphs, seemed intuitive and self-evident, but the counterexample found by the mathematicians challenges this assumption. The discovery not only offers insights into related problems in physics, but also raises questions about the role of intuition in mathematics. The bunkbed conjecture was first proposed by a Dutch physicist in the 1980s, and involves flipping coins to determine which edges to erase in a stacked graph. The probability of finding a path between two vertices in the bottom graph and its corresponding vertex in the top graph was thought to be the same as the probability of finding a path between the two vertices in the bottom graph alone. However, the counterexample found by the mathematicians proves otherwise. This discovery highlights the importance of questioning assumptions and the potential for unexpected results in mathematics.
